FFT & NTT 学习笔记 2021 年 7 月 22 日 以下是我对 FFT 的感性理解,可能并不严谨,如有错误欢迎指正。
FFT
以下讲述的算法是 Cooley–Tukey FFT,它在算法竞赛中使用的更为广泛。
前置知识:复数,需要理解 Euler 公式。
多项式乘法
对于 n n n
f ( x ) = ∑ i = 0 n f i x i = f 0 + f 1 x + f 2 x 2 + ⋯ + g n x n g ( x ) = ∑ i = 0 n g i x i = g 0 + g 1 x + g 2 x 2 + ⋯ + g n x n \begin{aligned}
f(x) = \sum_{i=0}^n f_ix^i &= f_0 + f_1 x + f_2x^2 + \cdots + g_nx^n \\
g(x) = \sum_{i=0}^n g_ix^i &= g_0 + g_1 x + g_2x^2 + \cdots + g_nx^n
\end{aligned} f ( x ) = i = 0 ∑ n f i x i g ( x ) = i = 0 ∑ n g i x i = f 0 + f 1 x + f 2 x 2 + ⋯ + g n x n = g 0 + g 1 x + g 2 x 2 + ⋯ + g n x n 它们的卷积是 F ( x ) = f ( x ) ∗ g ( x ) = ( f ∗ g ) ( x ) = ∑ k = 0 2 n c k x k F(x) = f(x) \ast g(x) = (f \ast g)(x) = \sum\limits_{k=0}^{2n} c_kx^k F ( x ) = f ( x ) ∗ g ( x ) = ( f ∗ g ) ( x ) = k = 0 ∑ 2 n c k x k
c k = ∑ i + j = k f i g j c_k = \sum_{i+j=k}f_ig_j c k = i + j = k ∑ f i g j 因此朴素的计算多项式的卷积需要 n 2 n^2 n 2
点值表示法
n n n f ( x ) f(x) f ( x ) n + 1 n+1 n + 1 n + 1 n+1 n + 1 n n n n + 1 n+1 n + 1
考虑选取 2 n + 1 2n+1 2 n + 1 f ( x ) f(x) f ( x ) g ( x ) g(x) g ( x ) F ( x ) F(x) F ( x ) 2 n + 1 2n+1 2 n + 1
( x k , F ( x k ) ) = ( x k , f ( x k ) g ( x k ) ) (x_k,F(x_k)) = \left(x_k, f(x_k)g(x_k)\right) ( x k , F ( x k )) = ( x k , f ( x k ) g ( x k ) ) 现在我们有了新的思路:先从系数表示法转换为点值表示法,做完乘法后再变回去。
DFT
怎么把多项式转换成点值呢?我们有离散 Fourier 变换。
称方程 x n = 1 x^n = 1 x n = 1 n n n ζ n \zeta_n ζ n f ( x ) = ∑ k = 0 n − 1 f k x k f(x) = \sum\limits_{k=0}^{n-1} f_kx^k f ( x ) = k = 0 ∑ n − 1 f k x k ζ n \zeta_n ζ n
DFT ζ n ( f ) = ( f ( 1 ) , f ( ζ n 1 ) , ⋯ , f ( ζ n n − 1 ) ) \operatorname{DFT}_{\zeta_n}(f) =( f(1), f(\zeta_n^1), \cdots, f(\zeta_n^{n-1}) ) DFT ζ n ( f ) = ( f ( 1 ) , f ( ζ n 1 ) , ⋯ , f ( ζ n n − 1 )) 为 f f f
DFT 存在逆变换(IDFT),即从点值重新变回系数,仍是从向量到向量的变换。
IDFT 具有一个关键性质
( DFT ζ ) − 1 = 1 n ( DFT ζ − 1 ) (1) (\operatorname{DFT}_{\zeta})^{-1} = \frac{1}{n} (\operatorname{DFT}_{{\zeta}^{-1}}) \tag{1} ( DFT ζ ) − 1 = n 1 ( DFT ζ − 1 ) ( 1 ) 我们将在后文证明它。现在我们可以统一的处理 DFT 和 IDFT。
为了方便描述,接下来我们将把 DFT ζ n \operatorname{DFT}_{\zeta_n} DFT ζ n F n \mathcal{F}_n F n
单位原根
至此,我们计算 DFT 的复杂度仍然是 O ( n 2 ) O(n^2) O ( n 2 )
单位根中特殊的一个记作 ζ n = e 2 π i n \zeta_n = e^{\frac{2 \pi i}{n}} ζ n = e n 2 πi
ζ n = e 2 π i n = cos ( 2 π n ) + i sin ( 2 π n ) \zeta_n = e^{\tfrac{2 \pi i}{n}} = \cos \left(\frac{2\pi}{n}\right) + i \sin \left(\frac{2\pi}{n}\right) ζ n = e n 2 πi = cos ( n 2 π ) + i sin ( n 2 π ) 即 ζ n \zeta_n ζ n n n n
x k = ζ n k = e k 2 π i n = cos ( 2 π k n ) + i sin ( 2 π k n ) x_k = \zeta_n^k = e^{k\tfrac{2 \pi i}{n}} = \cos \left(\frac{2\pi k}{n}\right) + i \sin \left(\frac{2\pi k}{n}\right) x k = ζ n k = e k n 2 πi = cos ( n 2 πk ) + i sin ( n 2 πk ) 恰对应到单位圆的 n n n 单位根之间的乘法就是在单位圆上转圈圈。
不难通过 Euler 公式验证单位原根 ζ n \zeta_n ζ n
ζ 2 n 2 k = ζ n k \zeta_{2n}^{2k} = \zeta_n^k ζ 2 n 2 k = ζ n k ζ 2 n n + k = − ζ 2 n k \zeta_{2n}^{n+k} = -\zeta_{2n}^k ζ 2 n n + k = − ζ 2 n k
分治
利用单位原根的特殊性,我们可以分治计算 DFT。比如对于 7 7 7
f ( x ) = f 0 + f 1 x + f 2 x 2 + f 3 x 3 + f 4 x 4 + f 5 x 5 + f 6 x 6 + f 7 x 7 = ( f 0 + f 2 x 2 + f 4 x 4 + f 6 x 6 ) + x ( f 1 + f 3 x 2 + f 5 x 4 + f 7 x 6 ) \begin{aligned}
f(x) &= f_0 + f_1x + f_2x^2 + f_3 x^3 + f_4 x^4 + f_5 x^5 + f_6 x^6 + f_7 x^7 \\
&= (f_0 + f_2x^2 + f_4x^4 + f_6x^6) + x(f_1 + f_3x^2 + f_5x^4 + f_7x^6)
\end{aligned} f ( x ) = f 0 + f 1 x + f 2 x 2 + f 3 x 3 + f 4 x 4 + f 5 x 5 + f 6 x 6 + f 7 x 7 = ( f 0 + f 2 x 2 + f 4 x 4 + f 6 x 6 ) + x ( f 1 + f 3 x 2 + f 5 x 4 + f 7 x 6 ) 奇偶分类
f [ 0 ] ( x ) = f 0 + f 2 x + f 4 x 2 + f 6 x 3 f [ 1 ] ( x ) = f 1 + f 3 x + f 5 x 2 + f 7 x 3 \begin{aligned}
f^{[0]}(x) &= f_0 + f_2x + f_4x^2 + f_6x^3 \\
f^{[1]}(x) &= f_1 + f_3x + f_5x^2 + f_7x^3
\end{aligned} f [ 0 ] ( x ) f [ 1 ] ( x ) = f 0 + f 2 x + f 4 x 2 + f 6 x 3 = f 1 + f 3 x + f 5 x 2 + f 7 x 3 则原来的函数可以表示为
f ( x ) = f [ 0 ] ( x 2 ) + x f [ 1 ] ( x 2 ) f(x) = f^{[0]}(x^2) + xf^{[1]}(x^2) f ( x ) = f [ 0 ] ( x 2 ) + x f [ 1 ] ( x 2 ) 一般的,对于度小于 n n n f ( x ) f(x) f ( x ) x = ζ n k x = \zeta_n^k x = ζ n k
f ( ζ n k ) = f [ 0 ] ( ζ n k ⋅ ζ n k ) + ζ n k f [ 1 ] ( ζ n k ⋅ ζ n k ) = f [ 0 ] ( ζ n 2 k ) + ζ n k f [ 1 ] ( ζ n 2 k ) = f [ 0 ] ( ζ n / 2 k ) + ζ n k f [ 1 ] ( ζ n / 2 k ) \begin{aligned}
f(\zeta_n^k) &= f^{[0]}(\zeta_n^k \cdot \zeta_n^k) + \zeta_n^kf^{[1]}(\zeta_n^k \cdot \zeta_n^k) \\
&= f^{[0]}(\zeta_n^{2k}) + \zeta_n^kf^{[1]}(\zeta_n^{2k}) \\
&= f^{[0]}(\zeta_{n/2}^{k}) + \zeta_n^kf^{[1]}(\zeta_{n/2}^{k})
\end{aligned} f ( ζ n k ) = f [ 0 ] ( ζ n k ⋅ ζ n k ) + ζ n k f [ 1 ] ( ζ n k ⋅ ζ n k ) = f [ 0 ] ( ζ n 2 k ) + ζ n k f [ 1 ] ( ζ n 2 k ) = f [ 0 ] ( ζ n /2 k ) + ζ n k f [ 1 ] ( ζ n /2 k ) 同理可得
f ( ζ n k + n / 2 ) = f [ 0 ] ( ζ n 2 k + n ) + ζ n k + n / 2 f [ 1 ] ( ζ n 2 k + n ) = f [ 0 ] ( ζ n / 2 k ) − ζ n k f [ 1 ] ( ζ n / 2 k ) \begin{aligned}
f(\zeta_n^{k+n/2}) &= f^{[0]}(\zeta_n^{2k+n}) + \zeta_n^{k+n/2}f^{[1]}(\zeta_n^{2k+n}) \\
&= f^{[0]}(\zeta_{n/2}^{k}) - \zeta_n^{k}f^{[1]}(\zeta_{n/2}^{k})
\end{aligned} f ( ζ n k + n /2 ) = f [ 0 ] ( ζ n 2 k + n ) + ζ n k + n /2 f [ 1 ] ( ζ n 2 k + n ) = f [ 0 ] ( ζ n /2 k ) − ζ n k f [ 1 ] ( ζ n /2 k ) 在 DFT 中使用有
F n ( f ) [ j ] = F n / 2 ( f [ 0 ] ) [ j ] + ζ n j F n / 2 ( f [ 1 ] ) [ j ] F n ( f ) [ j + n / 2 ] = F n / 2 ( f [ 0 ] ) [ j ] − ζ n j F n / 2 ( f [ 1 ] ) [ j ] (2) \begin{aligned}
\mathcal{F}_n(f)[j] &= \mathcal{F}_{n/2}(f^{[0]})[j] + \zeta_n^j \mathcal{F}_{n/2}(f^{[1]})[j] \\
\mathcal{F}_n(f)[j + n/2] &= \mathcal{F}_{n/2}(f^{[0]})[j] - \zeta_n^j\mathcal{F}_{n/2}(f^{[1]})[j]
\end{aligned}
\tag{2} F n ( f ) [ j ] F n ( f ) [ j + n /2 ] = F n /2 ( f [ 0 ] ) [ j ] + ζ n j F n /2 ( f [ 1 ] ) [ j ] = F n /2 ( f [ 0 ] ) [ j ] − ζ n j F n /2 ( f [ 1 ] ) [ j ] ( 2 ) 因此我们需要把多项式的系数个数向上补到 2 n 2^n 2 n
至此,我们可以写出递归版的 FFT。
void fft ( int n , img * f , int op ) { static img tmp[ 1 << 18 ]; if (n == 1 ) return ; for ( int i = 0 ; i < n; i ++ ) tmp[i] = f[i]; for ( int i = 0 ; i < n; i ++ ) { // 偶数放左边,奇数放右边 if (i & 1 ) f[n / 2 + i / 2 ] = tmp[i]; else f[i / 2 ] = tmp[i]; } img * g = f, * h = f + n / 2 ; fft (n / 2 , g, op), fft (n / 2 , h, op); img w0 = { cos ( 2 * PI / n), sin ( 2 * PI * op / n)}, w = { 1 , 0 }; for ( int k = 0 ; k < n / 2 ; k ++ ) { tmp[k] = g[k] + w * h[k]; tmp[k + n / 2 ] = g[k] - w * h[k]; w = w * w0; } for ( int i = 0 ; i < n; i ++ ) f[i] = tmp[i]; } 蝴蝶变换
递归分治总是不尽人意的,我们在前几行只是做了递归分组的事情,可以考虑一步到位。
还是以 7 7 7
初始 { x 0 , x 1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 } \{x^0,x^1,x^2,x^3,x^4,x^5,x^6,x^7\} { x 0 , x 1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 }
一次 { x 0 , x 2 , x 4 , x 6 } , { x 1 , x 3 , x 5 , x 7 } \{x^0,x^2,x^4,x^6\},\{x^1,x^3,x^5,x^7\} { x 0 , x 2 , x 4 , x 6 } , { x 1 , x 3 , x 5 , x 7 }
两次 { x 0 , x 4 } , { x 2 , x 6 } , { x 1 , x 5 } , { x 3 , x 7 } \{x^0,x^4\},\{x^2,x^6\},\{x^1,x^5\},\{x^3,x^7\} { x 0 , x 4 } , { x 2 , x 6 } , { x 1 , x 5 } , { x 3 , x 7 }
结束 { x 0 } , { x 4 } , { x 2 } , { x 6 } , { x 1 } , { x 5 } , { x 3 } , { x 7 } \{x^0\},\{x^4\},\{x^2\},\{x^6\},\{x^1\},\{x^5\},\{x^3\},\{x^7\} { x 0 } , { x 4 } , { x 2 } , { x 6 } , { x 1 } , { x 5 } , { x 3 } , { x 7 }
写出二进制的形式,可以发现:结束和开始的二进制恰好是相反的。
初始 0 1 2 3 4 5 6 7 初始(2) 000 001 010 011 100 101 110 111 结束(2) 000 100 010 110 001 101 011 111 结束 0 4 2 6 1 5 3 7
这个变换称为蝴蝶变换,也称位逆序置换(bit-reversal permutation)。
我们可以 O ( n ) O(n) O ( n ) R(x) 是 x x x R(x >> 1) 此时是已知的。即是把 R(x >> 1) 右移一位再补上最高位即可。代码如下
void pre_rev ( int lim ) { int k = std :: __lg (lim); rev. resize (lim); for ( int i = 0 ; i < lim; ++ i) { rev[i] = rev[i >> 1 ] >> 1 ; if (i & 1 ) rev[i] |= lim >> 1 ; // 或者合并写为 // rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (k - 1)); } } 现在我们可以写出非递归版的 FFT。
void fft ( img * f , int n , int op ) { // DIT for ( int i = 0 ; i < n; ++ i) if (i < rev[i]) swap (f[i], f[rev[i]]); for ( int l = 1 ; l <= n / 2 ; l <<= 1 ) { img w0 = { cos (PI / l), sin (PI * op / l)}; for ( int i = 0 ; i < n; i += l * 2 ) { img w = { 1 , 0 }; for ( int j = 0 ; j < l; j ++ ) { img x = f[i + j], y = w * f[i + j + l]; f[i + j] = x + y, f[i + j + l] = x - y; w = w * w0; } } } if (op == - 1 ) for ( int i = 0 ; i < n; i ++ ) f[i] = f[i] / n; } NTT
前置知识:数论基础(整除,同余)。
用 double 去实现整数的乘法是很不优美的,精度、速度都很成问题。实际上,我们可以仅在整数下进行运算。
原根
我们本质上用到的单位原根 ζ n \zeta_n ζ n
ζ n n = 1 \zeta_{n}^{n} = 1 ζ n n = 1 ζ 2 n n = − 1 \zeta_{2n}^{n} = -1 ζ 2 n n = − 1
可以联想到模 p p p Z p \mathbb{Z}_p Z p { 0 , 1 , ⋯ , p − 1 } \{0,1,\cdots,p-1\} { 0 , 1 , ⋯ , p − 1 } p p p
a φ ( p ) = a p − 1 ≡ 1 a^{\varphi(p)} = a^{p-1} \equiv 1 a φ ( p ) = a p − 1 ≡ 1 即从另一个角度说,p − 1 p-1 p − 1 x p − 1 ≡ 1 x^{p-1} \equiv 1 x p − 1 ≡ 1
它和单位根有很相似的形式,直觉上 Z p \mathbb{Z}_p Z p Z p \mathbb{Z}_p Z p
定义正整数 a ∈ Z p a \in \mathbb{Z}_p a ∈ Z p δ p ( a ) \delta_p(a) δ p ( a ) r r r a r ≡ 1 a^r \equiv 1 a r ≡ 1 a φ ( p ) ≡ 1 a^{\varphi(p)} \equiv 1 a φ ( p ) ≡ 1 a a a δ p ( a ) ∣ φ ( p ) \delta_p(a) \mid \varphi(p) δ p ( a ) ∣ φ ( p )
a , a 2 , ⋯ a δ p ( a ) (3) a,a^2,\cdots a^{\delta_p(a)} \tag{3} a , a 2 , ⋯ a δ p ( a ) ( 3 ) 在模 p p p x δ p ( a ) ≡ 1 x^{\delta_p(a)} \equiv 1 x δ p ( a ) ≡ 1 δ p ( a ) \delta_p(a) δ p ( a ) ( 3 ) (3) ( 3 )
通过整除的性质,可以想到只有 i ⊥ δ p ( a ) i \bot \delta_p(a) i ⊥ δ p ( a ) δ p ( a i ) = δ p ( a ) \delta_p(a^i) = \delta_p(a) δ p ( a i ) = δ p ( a ) a a a
∑ i = 1 δ p ( a ) [ gcd ( i , δ p ( a ) ) = 1 ] = φ ( δ p ( a ) ) \sum_{i=1}^{\delta_p(a)} [\gcd(i, \delta_p(a)) = 1] = \varphi(\delta_p(a)) i = 1 ∑ δ p ( a ) [ g cd( i , δ p ( a )) = 1 ] = φ ( δ p ( a )) 个阶相同的东西。因此阶为 δ p ( a ) \delta_p(a) δ p ( a ) φ ( δ p ( a ) ) \varphi(\delta_p(a)) φ ( δ p ( a ))
因为每个正整数都有唯一确定的阶,不妨假设对于所有 d ∣ φ ( p ) d \mid \varphi(p) d ∣ φ ( p ) d d d φ ( d ) \varphi(d) φ ( d )
∑ d ∣ φ ( p ) φ ( d ) = φ ( p ) = p − 1 \sum_{d \mid \varphi(p)} \varphi(d) = \varphi(p) = p - 1 d ∣ φ ( p ) ∑ φ ( d ) = φ ( p ) = p − 1 恰为 Z p \mathbb{Z}_p Z p a a a δ p ( a ) = p − 1 \delta_p(a) = p-1 δ p ( a ) = p − 1
我们称这个 a a a p p p g g g
快速数论变换
尽可能提取 p − 1 p - 1 p − 1 2 2 2
p = N q + 1 , N = 2 m p = N q + 1, N = 2^m p = Nq + 1 , N = 2 m 设 Z p \mathbb{Z}_p Z p g g g g N ≡ g q g_N \equiv g^q g N ≡ g q ζ n \zeta_n ζ n g N N ≡ 1 g_N^N \equiv 1 g N N ≡ 1 g N N / 2 ≡ − 1 g_N^{N/2} \equiv -1 g N N /2 ≡ − 1
常见的有
p = 1004535809 = 479 × 2 21 + 1 , g = 3 p = 998244353 = 7 × 17 × 2 23 + 1 , g = 3 \begin{aligned}
p = 1004535809 = 479 \times 2^{21} + 1&, g = 3 \\
p = 998244353 = 7 \times 17 \times 2^{23} + 1&, g = 3
\end{aligned} p = 1004535809 = 479 × 2 21 + 1 p = 998244353 = 7 × 17 × 2 23 + 1 , g = 3 , g = 3 类似的,我们可以写出程序
void ntt ( ll * f , int n , int type ) { for ( int i = 0 ; i < n; ++ i) if (i < rev[i]) swap (f[i], f[rev[i]]); for ( int h = 2 ; h < n; h <<= 1 ) { ll tg = type == 1 ? 3 : g_inv; ll gn = qpow (tg, (P - 1 ) / h); for ( int j = 0 ; j < n; j += h) { ll g = 1 ; for ( int k = j; k < j + h / 2 ; k ++ ) { ll f1 = f[k], f2 = g * f[k + h / 2 ] % P; f[k] = (f1 + f2) % P; f[k + h / 2 ] = (f1 - f2 + P) % P; g = g * gn % P; } } } ll iv_n = qpow (n); if (type == - 1 ) for ( int i = 0 ; i < n; i ++ ) f[i] = f[i] * iv_n % P; } 至此,你已经学会 FFT 了。下面我们将更深入的从数学角度研究 FFT,补足理论基础。
线性变换
DFT 是一个线性变换。换句话说,它可以被写成矩阵乘法的形式
[ f ( ζ n 0 ) f ( ζ n 1 ) f ( ζ n 2 ) ⋮ f ( ζ n n − 1 ) ] = [ 1 1 1 ⋯ 1 1 ζ n 1 ζ n 2 ⋯ ζ n n − 1 1 ζ n 2 ζ n 4 ⋯ ζ n 2 ( n − 1 ) ⋮ ⋮ ⋮ ⋱ ⋮ 1 ζ n n − 1 ζ n 2 ( n − 1 ) ⋯ ζ n ( n − 1 ) 2 ] [ f 0 f 1 f 2 ⋮ f n − 1 ] \begin{bmatrix}
f(\zeta_n^0) \\ f(\zeta_n^1) \\ f(\zeta_n^2) \\ \vdots \\ f(\zeta_n^{n-1})
\end{bmatrix} = \begin{bmatrix}
1 & 1 & 1 & \cdots & 1 \\
1 & \zeta_n^1 & \zeta_n^2 & \cdots & \zeta_n^{n-1} \\
1 & \zeta_n^2 & \zeta_n^4 & \cdots & \zeta_n^{2(n-1)} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & \zeta_n^{n-1} & \zeta_n^{2(n-1)} & \cdots & \zeta_n^{(n-1)^2}
\end{bmatrix}
\begin{bmatrix}
f_0 \\ f_1 \\ f_2 \\ \vdots \\ f_{n-1}
\end{bmatrix} f ( ζ n 0 ) f ( ζ n 1 ) f ( ζ n 2 ) ⋮ f ( ζ n n − 1 ) = 1 1 1 ⋮ 1 1 ζ n 1 ζ n 2 ⋮ ζ n n − 1 1 ζ n 2 ζ n 4 ⋮ ζ n 2 ( n − 1 ) ⋯ ⋯ ⋯ ⋱ ⋯ 1 ζ n n − 1 ζ n 2 ( n − 1 ) ⋮ ζ n ( n − 1 ) 2 f 0 f 1 f 2 ⋮ f n − 1 我们把中间的那个 n n n V ( ζ n ) = ( ζ n i j ) V(\zeta_n) = (\zeta_n^{ij}) V ( ζ n ) = ( ζ n ij )
直接计算 V ( ζ n ) V(\zeta_n) V ( ζ n )
V ( ζ n ) V ( ζ n − 1 ) = ( n [ i = j ] ) = n I n V(\zeta_n) V(\zeta_n^{-1}) = (n[i = j]) = n I_n V ( ζ n ) V ( ζ n − 1 ) = ( n [ i = j ]) = n I n 即 IDFT 所对应的矩阵为 V − 1 ( ζ n ) = 1 n V ( ζ n − 1 ) V^{-1}(\zeta_n) = \frac{1}{n} V(\zeta_n^{-1}) V − 1 ( ζ n ) = n 1 V ( ζ n − 1 ) ( 1 ) (1) ( 1 )
干掉 REV
其实上文所实现的 FFT 和 IFFT 并不对偶,只是卷积定理使得 IFFT 恰是 FFT 的逆运算。具体的说,我们实现了两个 DIT,因此需要在计算之前进行蝴蝶变换。
我们运算的核心内容在于 ( 2 ) (2) ( 2 )
[ O 1 O 2 ] = [ 1 ζ n − j 1 − ζ n − j ] [ I 1 I 2 ] \begin{bmatrix}
O_1 \\ O_2
\end{bmatrix} =
\begin{bmatrix}
1 & \zeta_n^{-j} \\
1 & -\zeta_n^{-j}
\end{bmatrix}
\begin{bmatrix}
I_1 \\ I_2
\end{bmatrix} [ O 1 O 2 ] = [ 1 1 ζ n − j − ζ n − j ] [ I 1 I 2 ] 对矩阵求逆
[ I 1 I 2 ] = 1 2 [ 1 1 ζ n j − ζ n j ] [ O 1 O 2 ] (4) \begin{bmatrix}
I_1 \\ I_2
\end{bmatrix} = \frac{1}{2}
\begin{bmatrix}
1 & 1 \\
\zeta_n^{j} & -\zeta_n^{j}
\end{bmatrix}
\begin{bmatrix}
O_1 \\ O_2
\end{bmatrix} \tag{4} [ I 1 I 2 ] = 2 1 [ 1 ζ n j 1 − ζ n j ] [ O 1 O 2 ] ( 4 ) 我们便得到了 DIF。类似的,我们可以实现两个 DIF 作为 FFT,此时蝴蝶变换在计算之后。
void fft ( img * f , int n , int op ) { // DIF for ( int l = n / 2 ; l >= 1 ; l >>= 1 ) { img w0 = { cos (PI / l), sin (PI * op / l)}; for ( int i = 0 ; i < n; i += l * 2 ) { img w = { 1 , 0 }; for ( int j = 0 ; j < l; j ++ ) { img x = f[i + j], y = f[i + j + l]; f[i + j] = x + y, f[i + j + l] = w * (x - y); w = w * w0; } } } for ( int i = 0 ; i < n; ++ i) if (i < rev[i]) swap (f[i], f[rev[i]]); if (op == - 1 ) for ( int i = 0 ; i < n; i ++ ) f[i] = f[i] / n; } 容易发现,若我们以 DIF 作为 FFT,DIT 作为 IFFT,是不需要蝴蝶变换的。
void fft ( img * f , int n ) { for ( int l = n / 2 ; l >= 1 ; l >>= 1 ) { img w0 = { cos (PI / l), sin (PI / l)}; for ( int i = 0 ; i < n; i += l * 2 ) { img w = { 1 , 0 }; for ( int j = 0 ; j < l; j ++ ) { img x = f[i + j], y = f[i + j + l]; f[i + j] = x + y, f[i + j + l] = w * (x - y); w = w * w0; } } } } void ifft ( img * f , int n ) { for ( int l = 1 ; l <= n / 2 ; l <<= 1 ) { img w0 = img{ cos (PI / l), sin (PI / l)}. conj (); for ( int i = 0 ; i < n; i += l * 2 ) { img w = { 1 , 0 }; for ( int j = 0 ; j < l; j ++ ) { img x = f[i + j], y = w * f[i + j + l]; f[i + j] = x + y, f[i + j + l] = x - y; w = w * w0; } } } for ( int i = 0 ; i < n; i ++ ) f[i] = f[i] / n; } 以上,便是 Twisted FFT。
另一种理解
注意到
f ( x 0 ) = f m o d ( x − x 0 ) f(x_0) = f \bmod (x - x_0) f ( x 0 ) = f mod ( x − x 0 ) 我们可以从这方面着手,从取模角度重新审视上述算法。假设 f f f
f = ( x n − r ) ( x n + r ) f 0 + ( x n − r ) f 1 + ( x n + r ) f 2 + f 3 f = (x^n - r)(x^n + r)f_{0} + (x^n - r)f_{1} + (x^n + r)f_{2} + f_3 f = ( x n − r ) ( x n + r ) f 0 + ( x n − r ) f 1 + ( x n + r ) f 2 + f 3 令
O 1 = f m o d ( x n + r ) = − 2 r f 1 + f 3 O 2 = f m o d ( x n − r ) = 2 r f 2 + f 3 \begin{aligned}
O_1 &= f \bmod (x^n + r) = -2r f_1 + f_3\\
O_2 &= f \bmod (x^n - r) = 2r f_2 + f_3
\end{aligned} O 1 O 2 = f mod ( x n + r ) = − 2 r f 1 + f 3 = f mod ( x n − r ) = 2 r f 2 + f 3 故
f m o d ( x 2 n − r 2 ) = O 2 − O 1 2 r x n + O 2 + O 1 2 = I 1 x n + I 2 f \bmod (x^{2n} - r^2) = \frac{O_2-O_1}{2r}x^n + \frac{O_2 + O_1}{2} = I_1 x^n + I_2 f mod ( x 2 n − r 2 ) = 2 r O 2 − O 1 x n + 2 O 2 + O 1 = I 1 x n + I 2 注意到代码中我们并没有直接求 O 1 O_1 O 1 j j j ζ 2 n j \zeta_{2n}^j ζ 2 n j f ( ζ 2 n x ) f(\zeta_{2n}x) f ( ζ 2 n x )
可以发现
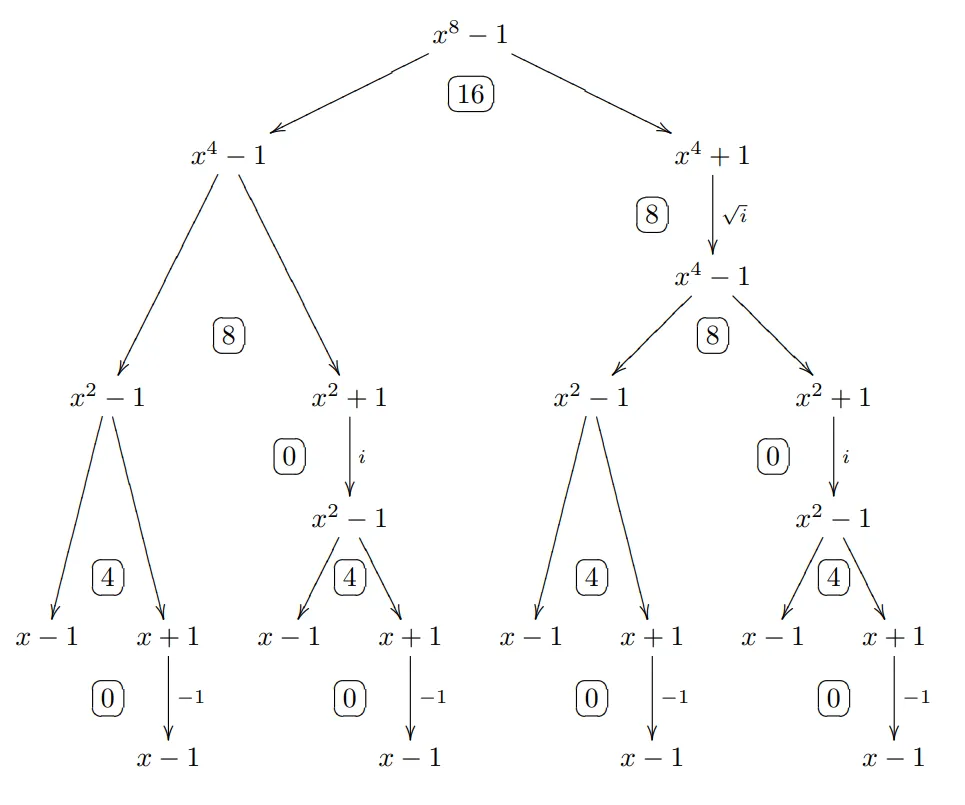
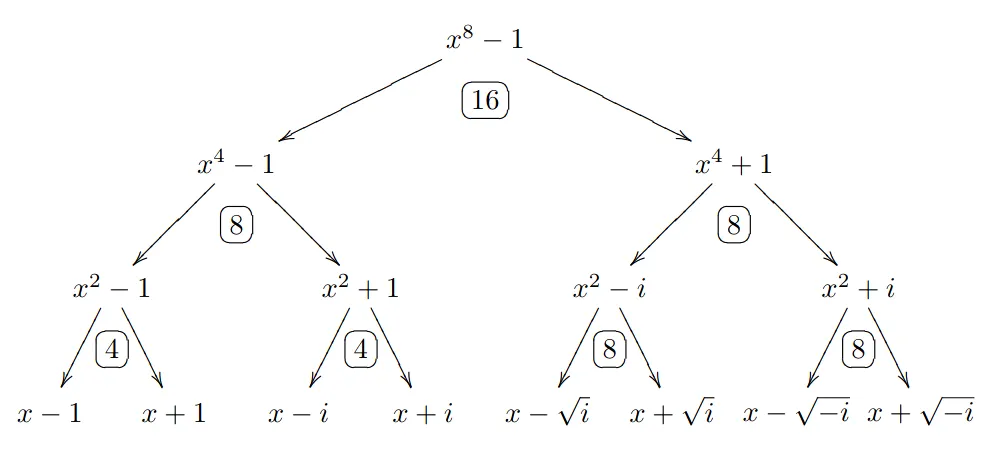
f ( ζ 2 n x ) m o d ( x n − 1 ) = f ( ζ 2 n x ) m o d ( ( ζ 2 n x ) n − 1 ) = f ( x ) m o d ( x n + 1 ) f(\zeta_{2n}x) \bmod (x^n-1) = f(\zeta_{2n}x) \bmod ((\zeta_{2n} x)^n - 1) = f(x) \bmod (x^n + 1) f ( ζ 2 n x ) mod ( x n − 1 ) = f ( ζ 2 n x ) mod (( ζ 2 n x ) n − 1 ) = f ( x ) mod ( x n + 1 ) 这个图并不好理解,下面那张 Original FFT 更容易理解,但是现在广为流传的算法是 Twisted FFT。
通过图可以看出,FFT 的过程即是先把多项式从根推到叶子,即求得所有单位根处的值,做完操作后,再从叶子推回根。
Original FFT
当然,我们可以直接分治,便是 Original FFT。
由于篇幅有限,本文不展开。
预处理单位根
每次计算都重新计算一遍单位根太浪费了,我们可以预处理它,从而在计算中调用。
vector < img > ROOT; void init ( int n ) { static int lim = (ROOT = {{ 1 , 0 }}, 1 ); if (lim >= n) return ; ROOT. resize (n); for ( int l = lim; l < n; l *= 2 ) { img w = { cos (PI / l / 2 ), sin (PI / l / 2 )}; ROOT[l] = w; for ( int i = 1 ; i < l; ++ i) ROOT[i + l] = ROOT[i] * w; } lim = n; } 其他应用
FFT 实际上是一个工具,用于快速计算卷积,这篇文章我想更聚焦于理解 FFT 的计算过程。
FFT 还有很多应用,比如快速加法,带通配文本匹配等,后面等再刷些题了可能会开一篇讲一讲这个,现在我积累的还不够。
Refence
OI-Wiki 快速傅里叶变换 FFT 入门笔记 - hly1024