快读优化：无符号整数解析的几种 trick

2024 年 2 月 16 日

代码仓库：github/bench-int-parse。

学习性能分析的小作业。

即 OIer/ACMer 常说的快读。本文测试了一种另类且易于实现的快读，结果表明快 50% 左右。

在开始之前，我对问题做以下约束：

输入是类似 0 123\n456 123456789 的字符串，仅包含 ascii 字符
数字的范围是 $[0, 10^{18}]$ ，不考虑 u64 边界
实际中一般只有单个间隔符，但也要能够正确处理多个间隔符
在 O2 或者 O3 优化等级下进行测试
依据输入的性质，特化两种算法：
- 严格：输入是 ascii 字符
- 非严格（TODO）：仅有数字字符的值大于 0x30

接下来我将做几种实现，并使用 nanobench 库来进行性能测试。

一号选手：isdigit

最常见的快读往往使用 isdigit 或者等价的 '0' <= c && c <= '9' 来进行实现。

常见的快读长这样：

inline static u64 isd_0_getu(const char *&p) {
  char c = *p++;
  while (!std::isdigit(c))
    c = *p++;
  u64 x = c - '0';
  for (c = *p++; std::isdigit(c); c = *p++)
    x = x * 10 + c - '0';
  return x;
}

接下来对单间隔符，瞎写了种优化：

inline static u64 isd_1_getu(const char *&p) {
  while (true) {
    char c = *p++;
    if (std::isdigit(c)) {
      u64 x = c - '0';
      for (c = *p++; std::isdigit(c); c = *p++)
        x = x * 10 + c - '0';
      return x;
    }
  }
}

江湖上还流传一些“优化”，我也尝试实现了其中部分：

isd-0 ：上文中的 isdigit_0_getu
isd-1 ：上文中的 isdigit_1_getu
isd-u8 ：用 u8 存 char
isd-m10：把乘 10 写成 (c << 3) + (c << 1)
isd-and：把 c - '0' 写成 c & 0xf
isd-xor：把 c - '0' 写成 c ^ '0'
isd-range：把 isdigit 写成 '0' <= c && c <= '9'
isd-sub：把 isdigit 写成 u8(c - '0') <= 9，后面还可以省一次减法
isd-goto：不用循环，用 goto 来书写逻辑。
isd-sub-1：把上面跑得快的实现杂交一下
isd-sub-2：循环展开 20 次

性能测试

具体的测试方法见后文，这里只展示在 gcc -O2 下的结果（单位 us）。

算法/长度	1	2	4	8	12	16
isd-0	1057	1757	3145	6086	8854	11569
isd-1	1056	1638	3029	5917	8715	11452
isd-u8	881	1322	2627	4948	7863	10403
isd-m10	881	1322	2628	4963	7885	10404
isd-and	924	1322	2633	5151	7942	10271
isd-xor	1057	1499	3715	5630	8356	11253
isd-range	881	1371	2393	4853	7162	9851
isd-range-1	793	1295	2360	4811	7720	9978
isd-sub	793	1410	2637	5145	7831	10637
isd-goto	801	1453	2652	4749	8107	10639
isd-sub-1	793	1293	2389	4768	7842	9791
isd-sub-2	797	1321	2194	4198	6567	8923

据此，我们可以得到一些结论：

性能基本相近，短数字略有差距
isd-m10 与 isd-u8 生成的汇编完全相同
- lea 指令非常强大，能够完成加乘混合计算，比如 x * 10 + c - '0' 仅需两条指令
isd-xor 异或可能会让性能略降
isd-range 编译器把范围判断优化成减法判断，且减法使用 lea 而不是 sub，性能有神秘提升
isd-sub 看似优化了一次减法，但是 movzbl 只加载到 eax，仍需要一条指令扩充至 64 位，在本地 and 莫名更快

接下来仅保留部分作为代表继续参与测试。

二号选手：SWAR（SIMD within a Register）

举个例子，字符串 "42" 读取为 u16 是 0x3234（默认小端），即 0x0204。我们需要一个类似 (x << 8) * 10 + x 的操作让高位与低位正确的合并。

整理一下就是乘以 0x0a01。即 0x0204 * 0x0a01 = 0x142a04，目标值 0x2a = 42 就在其中。类似的，我们可以设计实现 u32 或 u64 乃至更长的合并。

推荐阅读：Faster Integer Parsing，图很直观。

不足长

对于不足长的字符串，我们还得再想想办法。

合法的数字仅在 0x30 到 0x39 之间，因此仅有数字 y = x & (x + 6) 仍以 0x30 开头；
再经过 z = (y & 0xf0f0) ^ 0x3030，把数字位归零；
借助于位运算魔法，len = std::countl_zero(z) >> 3；
最后使用 u = x >> (16 - (len << 3))，把数字对齐。

另外，std::countl_zero 比 ctz 指令多了特判 0，编译器会为此优化生成快速路径，性能数据会在此跳跃。此处我选择了手工处理。

总之，我们可以比较容易的对 16、32、64 字长进行实现。这里仅展示 u64 实现。

inline static u64 _swar_64(u64 u) {
  u = (u & 0x0f0f0f0f0f0f0f0f) * 0x0a01 >> 0x08;
  u = (u & 0x00ff00ff00ff00ff) * 0x00640001 >> 0x10;
  u = (u & 0x0000ffff0000ffff) * 0x271000000001 >> 0x20;
  return u;
}

inline static u64 swar_64_getu(const char *&p) {
  u64 x = 0;
  while (u8(*p - '0') > 9)
    p++;
  constexpr u32 p10[] = {1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000};
  constexpr u64 cx30 = 0x3030303030303030;
  while (true) {
    u64 u = *reinterpret_cast<const u64 *>(p);
    u64 umask = u & (u + 0x0606060606060606) & 0xf0f0f0f0f0f0f0f0;
    if (umask == cx30) {
      p += 8;
      x = x * p10[8] + _swar_64(u);
    } else {
      u64 len = std::countr_zero(umask ^ cx30) >> 3;
      if (len != 0) {
        u <<= 64 - (len << 3);
        p += len;
        x = x * p10[len] + _swar_64(u);
      }
      break;
    }
  }
  p++;
  return x;
}

我也尝试使用 AVX2 指令集进行实现，但是因为乘法位数不够，上述操作很难向量化，我的简陋实现的性能表现非常差，就不放出来丢脸了。

三号选手：打表

比性能怎么少得了打表呢！

预处理一个字符串 u16 到数值的表即可，再对边界情况判断一下。

template <class T>
T *_prepare_16_table() {
  constexpr u32 N = 0x10000;
  T *f = new T[N];
  std::memset(f, -1, N);
  for (u32 i = 0; i != 0x100; ++i) {
    for (u32 j = 0; j != 10; ++j) {
      u32 t = i * 0x100 | j | 0x30;
      if ('0' <= i && i <= '9')
        f[t] = j * 10 + i - 0x30;
      else
        f[t] = j | 0x100;
    }
  }
  return f;
}

inline u64 pre_16_getu(const char *&p) {
  static const auto *pre16 = _prepare_16_table<u16>();
  u8 c = *p++ - '0';
  while (c > 9)
    c = *p++ - '0';
  u64 x = c;
  while (true) {
    u16 t = *reinterpret_cast<const u16 *>(p);
    auto ft = pre16[t];
    p += 2;
    if (ft < 100) { // len = 2
      x = x * 100 + ft;
    } else { // len = 1
      if (ft < 0x1000)
        x = x * 10 + ft - 0x100;
      else
        --p;
      break;
    }
  }
  return x;
}

性能分析

测试方法：解析包含 $2^{20}$ 个数字的字符串，禁止循环展开（nounroll）。

性能表现

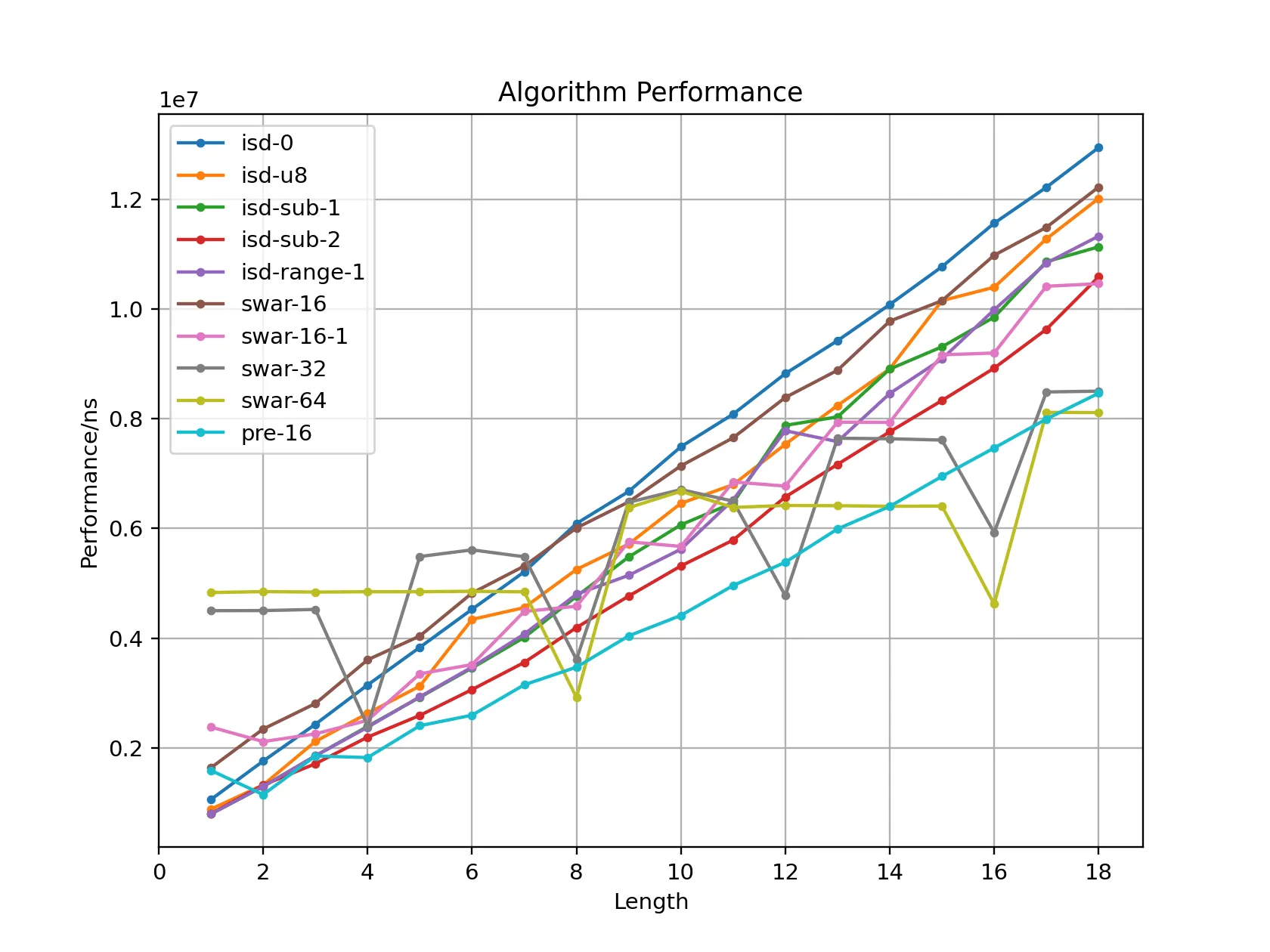
我们可以分析出以下结论：

以 isd-0 为基准，sub-2 的效率约为 122%，还是有一定的性能提升的。
swar 系在长数字情形下表现下十分优秀，例如 swar-64 效率可达 159%，在 len = 16 处更是高达 250%，但是 len = 1 处仅有 21%，短数字开销过大。
pre-16 有更好的常数，中长数字下的效率约为 152%。

总之，我选择 pre-16 作为最终实现。

后记